8.9.3.5 IfcBSplineCurve

ABSTRACT This definition may not be instantiated

8.9.3.5.1 Semantic definition

The IfcBSplineCurve is a spline curve parameterized by spline functions.

Figure 8.9.3.5.A illustrates a B-spline curve.

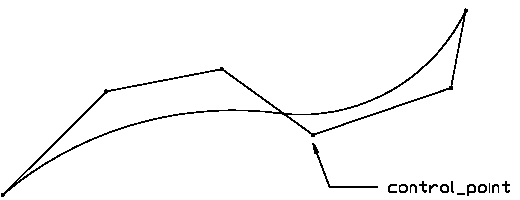
A B-spline curve is a piecewise parametric polynomial or rational curve described in terms of control points and basis functions. The B-spline curve has been selected as the most stable format to represent all types of polynomial or rational parametric curves. With appropriate attribute values it is capable of representing single span or spline curves of explicit polynomial, rational, Bezier or B-spline type.

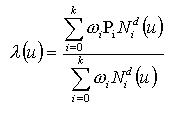
equation1 — Figure 8.9.3.5.B - Equation 1

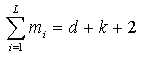
equation2 — Figure 8.9.3.5.C - Equation 2

Variable	Definition
k+1	Number of control points
P_i	Control points
w_i	Weights
d	Degree

Table 8.9.3.5.D - Variable definitions

Interpretation of the data is as follows:

All weights shall be positive and the curve is given by Figure 8.9.3.5.B, with variables defined in Table 8.9.3.5.D. The knot array is an array of (k+d+2) real numbers [u_-d ... u_k+1], such that for all indices j in [-d,k], u_j <= u_j+1. This array is obtained from the knot data list by repeating each multiple knot according to the multiplicity. N ^d_i, the ith normalized B-spline basis function of degree d, is defined on the subset [u_i-d, ... , u_i+1] of this array.
Let L denote the number of distinct values among the d+k+2 knots in the knot array; L will be referred to as the 'upper index on knots'. Let m_j denote the multiplicity (number of repetitions) of the jth distinct knot. Then see Figure 8.9.3.5.C. All knot multiplicities except the first and the last shall be in the range 1 ... degree; the first and last may have a maximum value of degree + 1. In evaluating the basis functions, a knot u of e.g. multiplicity 3 is interpreted as a string u, u, u, in the knot array. The B-spline curve has 3 special subtypes (Note: only 1, Bezier curve, included in this IFC release) where the knots and knot multiplicities are derived to provide simple default capabilities.
Logical flag is provided to indicate whether the curve self intersects or not.

8.9.3.5.2 Entity inheritance

8.9.3.5.3 Attributes

#	Attribute	Type	Description
IfcRepresentationItem (2)
	LayerAssignment	SET [0:1] OF IfcPresentationLayerAssignment FOR AssignedItems	Assignment of the representation item to a single or multiple layer(s). The LayerAssignments can override a LayerAssignments of the IfcRepresentation it is used within the list of Items. IFC2x3-CHANGE The inverse attribute LayerAssignments has been added. IFC4-CHANGE The inverse attribute LayerAssignment has been restricted to max 1. Upward compatibility for file based exchange is guaranteed.
	StyledByItem	SET [0:1] OF IfcStyledItem FOR Item	Reference to the IfcStyledItem that provides presentation information to the representation, e.g. a curve style, including colour and thickness to a geometric curve. IFC2x3-CHANGE The inverse attribute StyledByItem has been added.
IfcCurve (1)
*	Dim	IfcDimensionCount	This attribute is formally derived. `IfcCurveDim(SELF)` The space dimensionality of this abstract class, defined differently for all subtypes, i.e. for IfcLine, IfcConic and IfcBoundedCurve.
Click to show 3 hidden inherited attributes Click to hide 3 inherited attributes
IfcBSplineCurve (7)
1	Degree	IfcInteger	The algebraic degree of the basis functions.
2	ControlPointsList	LIST [2:?] OF IfcCartesianPoint	The list of control points for the curve.
3	CurveForm	IfcBSplineCurveForm	Used to identify particular types of curve; it is for information only.
4	ClosedCurve	IfcLogical	Indication of whether the curve is closed; it is for information only.
5	SelfIntersect	IfcLogical	Indication whether the curve self-intersects or not; it is for information only.
*	UpperIndexOnControlPoints	IfcInteger	This attribute is formally derived. `(SIZEOF(ControlPointsList) - 1)` The upper index on the array of control points; the lower index is 0. This value is derived from the control points list.
*	ControlPoints	ARRAY [0:UpperIndexOnControlPoints] OF IfcCartesianPoint	This attribute is formally derived. `IfcListToArray(ControlPointsList,0,UpperIndexOnControlPoints)` The array of control points used to define the geometry of the curve. This is derived from the list of control points.

Table 8.9.3.5.E

8.9.3.5.4 Formal propositions

Name	Description
SameDim	All control points shall have the same dimensionality.
`SIZEOF(QUERY(Temp <* ControlPointsList \| Temp.Dim <> ControlPointsList[1].Dim)) = 0`

Table 8.9.3.5.F

8.9.3.5.5 Formal representation

ENTITY IfcBSplineCurve
 ABSTRACT SUPERTYPE OF (ONEOF
	(IfcBSplineCurveWithKnots))
 SUBTYPE OF (IfcBoundedCurve);
	Degree : IfcInteger;
	ControlPointsList : LIST [2:?] OF IfcCartesianPoint;
	CurveForm : IfcBSplineCurveForm;
	ClosedCurve : IfcLogical;
	SelfIntersect : IfcLogical;
 DERIVE
	 UpperIndexOnControlPoints : IfcInteger := (SIZEOF(ControlPointsList) - 1);
	 ControlPoints : ARRAY [0:UpperIndexOnControlPoints] OF IfcCartesianPoint := IfcListToArray(ControlPointsList,0,UpperIndexOnControlPoints);
 WHERE
	SameDim : SIZEOF(QUERY(Temp <* ControlPointsList |
  Temp.Dim <> ControlPointsList[1].Dim))
= 0;
END_ENTITY;