8.20.3.5 IfcEdgeCurve
8.20.3.5.1 Semantic definition
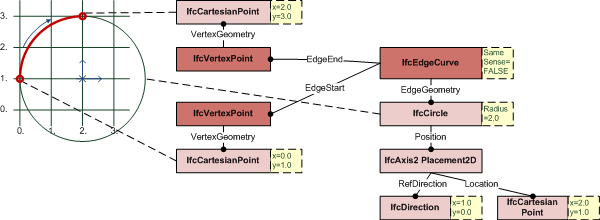
An IfcEdgeCurve defines two vertices being connected topologically including the geometric representation of the connection.
Informal Propositions
- The domain of the edge curve is formally defined to be the domain of its edge geometry as trimmed by the vertices. This domain does not include the vertices.
- An edge curve has non-zero finite extent.
- An edge curve is a manifold.
- An edge curve is arcwise connected.
- The edge start is not a part of the edge domain.
- The edge end is not a part of the edge domain.
- Vertex geometry shall be consistent with edge geometry.
8.20.3.5.2 Entity inheritance
8.20.3.5.3 Attributes
| # | Attribute | Type | Description |
|---|---|---|---|
| IfcRepresentationItem (2) | |||
| LayerAssignment | SET [0:1] OF IfcPresentationLayerAssignment FOR AssignedItems |
Assignment of the representation item to a single or multiple layer(s). The LayerAssignments can override a LayerAssignments of the IfcRepresentation it is used within the list of Items. |
|
| StyledByItem | SET [0:1] OF IfcStyledItem FOR Item |
Reference to the IfcStyledItem that provides presentation information to the representation, e.g. a curve style, including colour and thickness to a geometric curve. |
|
| IfcEdge (2) | |||
| 1 | EdgeStart | IfcVertex |
Start point (vertex) of the edge. |
| 2 | EdgeEnd | IfcVertex |
End point (vertex) of the edge. The same vertex can be used for both EdgeStart and EdgeEnd. |
| Click to show 4 hidden inherited attributes Click to hide 4 inherited attributes | |||
| IfcEdgeCurve (2) | |||
| 3 | EdgeGeometry | IfcCurve |
The curve which defines the shape and spatial location of the edge. This curve may be unbounded and is implicitly trimmed by the vertices of the edge; this defines the edge domain. Multiple edges can reference the same curve. |
| 4 | SameSense | IfcBoolean |
This logical flag indicates whether (TRUE), or not (FALSE) the senses of the edge and the curve defining the edge geometry are the same. The sense of an edge is from the edge start vertex to the edge end vertex; the sense of a curve is in the direction of increasing parameter. |
8.20.3.5.4 Examples
8.20.3.5.5 Formal representation
ENTITY IfcEdgeCurve
SUBTYPE OF (IfcEdge);
EdgeGeometry : IfcCurve;
SameSense : IfcBoolean;
END_ENTITY;
