8.9.3.7 IfcBSplineSurface

AbV ⓘ

ABSTRACT This definition may not be instantiated

8.9.3.7.1 Semantic definition

The IfcBSplineSurface is a general form of rational or polynomial parametric surface.

The symbology used here is:

Variable	Definition
K1	upper_index_on_u_control_points
K2	upper_index_on_v_control_points
P_ij	control_points
w_ij	weights
d1	u_degree
d2	v_degree

Table 8.9.3.7.D

The control points are ordered as: P₀₀, P₀₁, P₀₂, ..., P_K1(K2-1), P_K1K2

The weights, in the case of the rational subtype, are ordered similarly.

For each parameter, s = u or v, if k is the upper index on the control points and d is the degree for s, the knot array is an array of (k + d + 2) real numbers [s_-d, ...., s_k+1], such that for all indices j in [-d, k]; s_j ≤ s_j+1. This array is obtained from the appropriate u_knots or v_knots list by repeating each multiple knot according to the multiplicity.

N_i^d, the ith normalised B-spline basis function of degree d, is defined on the subset [s_i-d, ...., s_i+1] of this array.

Let L denote the number of distinct values amongst the knots in the knot list; L will be referred to as the ‘upper index on knots’. Let m_j denote the multiplicity (i.e., number of repetitions) of the jth distinct knot value. Then:

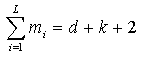
All knot multiplicities except the first and the last shall be in the range 1, ...., d; the first and last may have a maximum value of d+1. In evaluating the basis functions, a knot u of, e.g., multiplicity 3 is interpreted as a sequence u, u, u, in the knot array.

The surface form is used to identify specific quadric surface types (which shall have degree two), ruled surfaces and surfaces of revolution. As with the b-spline curve, the surface form is informational only and the spline data takes precedence.

The surface is to be interpreted as follows: In the polynomial case the surface is given by the equation:

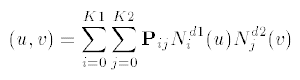
In the rational case the surface equation is:

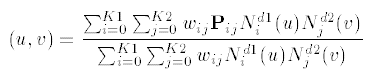
8.9.3.7.2 Entity inheritance

8.9.3.7.3 Attributes

#	Attribute	Type	Description
IfcRepresentationItem (2)
	LayerAssignment	SET [0:1] OF IfcPresentationLayerAssignment FOR AssignedItems	Assignment of the representation item to a single or multiple layer(s). The LayerAssignments can override a LayerAssignments of the IfcRepresentation it is used within the list of Items. IFC2x3-CHANGE The inverse attribute LayerAssignments has been added. IFC4-CHANGE The inverse attribute LayerAssignment has been restricted to max 1. Upward compatibility for file based exchange is guaranteed.
	StyledByItem	SET [0:1] OF IfcStyledItem FOR Item	Reference to the IfcStyledItem that provides presentation information to the representation, e.g. a curve style, including colour and thickness to a geometric curve. IFC2x3-CHANGE The inverse attribute StyledByItem has been added.
IfcSurface (1)
*	Dim	IfcDimensionCount	This attribute is formally derived. `3` The space dimensionality of IfcSurface. It is always a three-dimensional geometric representation item. IFC4-CHANGE Derived attribute promoted from subtypes.
Click to show 3 hidden inherited attributes Click to hide 3 inherited attributes
IfcBSplineSurface (10)
1	UDegree	IfcInteger	Algebraic degree of basis functions in u.
2	VDegree	IfcInteger	Algebraic degree of basis functions in v.
3	ControlPointsList	LIST [2:?] OF LIST [2:?] OF IfcCartesianPoint	This is a list of lists of control points.
4	SurfaceForm	IfcBSplineSurfaceForm	Indicator of special surface types.
5	UClosed	IfcLogical	Indication of whether the surface is closed in the u direction; this is for information only.
6	VClosed	IfcLogical	Indication of whether the surface is closed in the v direction; this is for information only.
7	SelfIntersect	IfcLogical	Flag to indicate whether, or not, surface is self-intersecting; this is for information only.
*	UUpper	IfcInteger	This attribute is formally derived. `SIZEOF(ControlPointsList) - 1` Upper index on control points in u direction.
*	VUpper	IfcInteger	This attribute is formally derived. `SIZEOF(ControlPointsList[1]) - 1` Upper index on control points in v direction.
*	ControlPoints	ARRAY [0:UUpper] OF ARRAY [0:VUpper] OF IfcCartesianPoint	This attribute is formally derived. `IfcMakeArrayOfArray(ControlPointsList, 0,UUpper,0,VUpper)` Array (two-dimensional) of control points defining surface geometry. This array is constructed from the control points list.

Table 8.9.3.7.E

8.9.3.7.4 Formal representation

ENTITY IfcBSplineSurface
 ABSTRACT SUPERTYPE OF (ONEOF
	(IfcBSplineSurfaceWithKnots))
 SUBTYPE OF (IfcBoundedSurface);
	UDegree : IfcInteger;
	VDegree : IfcInteger;
	ControlPointsList : LIST [2:?] OF LIST [2:?] OF IfcCartesianPoint;
	SurfaceForm : IfcBSplineSurfaceForm;
	UClosed : IfcLogical;
	VClosed : IfcLogical;
	SelfIntersect : IfcLogical;
 DERIVE
	 UUpper : IfcInteger := SIZEOF(ControlPointsList) - 1;
	 VUpper : IfcInteger := SIZEOF(ControlPointsList[1]) - 1;
	 ControlPoints : ARRAY [0:UUpper] OF ARRAY [0:VUpper] OF IfcCartesianPoint := IfcMakeArrayOfArray(ControlPointsList,
0,UUpper,0,VUpper);
END_ENTITY;