8.9.3.32 IfcEllipse
8.9.3.32.1 Semantic definition
An IfcEllipse is a curve consisting of a set of points whose distances to two fixed points add to the same constant.
The inherited SELF\IfcConic.Position.Location is the center of the IfcEllipse, and the inherited SELF\IfcConic.Position.P[1] is the direction of the SemiAxis1.
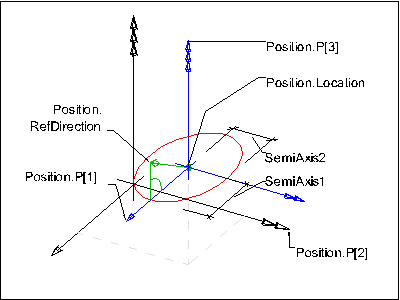
Definition of the IfcEllipse within the a three-dimensional position coordinate system is shown in Figure 8.9.3.32.A.
It is placed within the object coordinate system of an element of which it is a representation.
An ellipse is a conic section defined by the lengths of the semi-major and semi-minor diameters and the position (center or mid point of the line joining the foci) and orientation of the curve. Interpretation of the data shall be as follows:
C = SELF\IfcConic.Position.Location
x = SELF\IfcConic.Position.P[1]
y = SELF\IfcConic.Position.P[2]
z = SELF\IfcConic.Position.P[3]
R1 = SemiAxis1
R2 = SemiAxis2
The ellipse is parameterized as:
$$ \lambda(u) = C + (R_1\cos(u))x + (R_2\sin(u))y $$
The parameterization range is 0 ≤ u <≤ 2π (0 ≤ u ≤ 360 degree). In the placement coordinate system defined above, the ellipse is the equation C = 0, where
$$ C(x,y,z) = \frac{x^2}{R_1^2} + \frac{y^2}{R_2^2} - 1 $$
The positive sense of the ellipse at any point is in the tangent direction, T, to the curve at the point, where
$$ T = (-C_y,C_x,0) $$
8.9.3.32.2 Entity inheritance
-
- IfcCurve
- IfcAnnotationFillArea
- IfcBooleanResult
- IfcBoundingBox
- IfcCartesianPointList
- IfcCartesianTransformationOperator
- IfcCsgPrimitive3D
- IfcDirection
- IfcFaceBasedSurfaceModel
- IfcFillAreaStyleHatching
- IfcFillAreaStyleTiles
- IfcGeometricSet
- IfcHalfSpaceSolid
- IfcLightSource
- IfcPlacement
- IfcPlanarExtent
- IfcPoint
- IfcSectionedSpine
- IfcSegment
- IfcShellBasedSurfaceModel
- IfcSolidModel
- IfcSurface
- IfcTessellatedItem
- IfcTextLiteral
- IfcVector
8.9.3.32.3 Attributes
| # | Attribute | Type | Description |
|---|---|---|---|
| IfcRepresentationItem (2) | |||
| LayerAssignment | SET [0:1] OF IfcPresentationLayerAssignment FOR AssignedItems |
Assignment of the representation item to a single or multiple layer(s). The LayerAssignments can override a LayerAssignments of the IfcRepresentation it is used within the list of Items. |
|
| StyledByItem | SET [0:1] OF IfcStyledItem FOR Item |
Reference to the IfcStyledItem that provides presentation information to the representation, e.g. a curve style, including colour and thickness to a geometric curve. |
|
| IfcCurve (1) | |||
| * | Dim | IfcDimensionCount |
This attribute is formally derived. The space dimensionality of this abstract class, defined differently for all subtypes, i.e. for IfcLine, IfcConic and IfcBoundedCurve. |
| IfcConic (1) | |||
| 1 | Position | IfcAxis2Placement |
The location and orientation of the conic. Further details of the interpretation of this attribute are given for the individual subtypes." |
| Click to show 4 hidden inherited attributes Click to hide 4 inherited attributes | |||
| IfcEllipse (2) | |||
| 2 | SemiAxis1 | IfcPositiveLengthMeasure |
The first radius of the ellipse which shall be positive. Placement.Axes[1] gives the direction of the SemiAxis1. |
| 3 | SemiAxis2 | IfcPositiveLengthMeasure |
The second radius of the ellipse which shall be positive. |
8.9.3.32.4 Examples
8.9.3.32.5 Formal representation
ENTITY IfcEllipse
SUBTYPE OF (IfcConic);
SemiAxis1 : IfcPositiveLengthMeasure;
SemiAxis2 : IfcPositiveLengthMeasure;
END_ENTITY;