8.8.3.47 IfcTriangulatedFaceSet

RV ⓘ

AbV ⓘ

8.8.3.47.1 Semantic definition

The IfcTriangulatedFaceSet is a tessellated face set with all faces being bound by triangles. The faces are constructed by implicit polylines defined by three Cartesian points. Depending on the value of the inherited attribute Closed the instance of IfcTriangulatedFaceSet represents:

if TRUE, a boundary representation (or B-rep);
if FALSE, a face based surface representation.

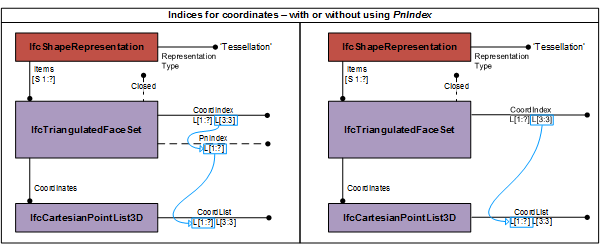
The coordinates of each point are provided by a one-based index into an ordered list of Cartesian points provided by the two-dimensional list CoordIndex, where

the first dimension of the two-dimensional list addresses the list of triangular faces;
the second dimension of the two-dimensional list provides exactly three indices. Each index points to a Cartesian point being a vertex of the triangle.

Depending on the provision of PnIndex the indices point either directly into the IfcCartesianPointList3D referenced by Coordinates defined at the supertype IfcTessellatedFaceSet, or they point into the PnIndex where the integer values at that position provides the location of the coordinate values within the IfcCartesianPointList3D. See Figure 8.8.3.47.A for the handling of point index.

IfcTriangulatedFaceSet_01 — Figure 8.8.3.47.A — Use of _PnIndex_

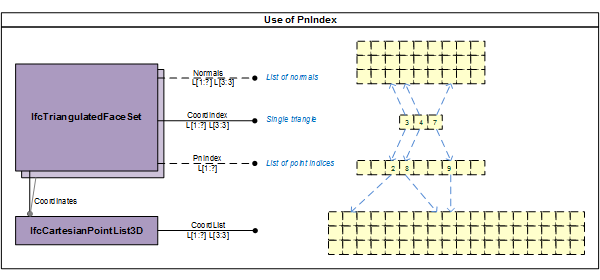
See Figure 8.8.3.47.B for using the IfcTriangulatedFaceSet without (as default) and with using the PnIndex.

IfcTriangulatedFaceSet_02 — Figure 8.8.3.47.B — Triangulated face set

Optionally normals can be provided. Only normals per vector are supported allowing for visually curved triangles when the three normals of the corresponding three vertices of a triangle are not co-linear to the normal of the triangular face. If they are identical, normals shall be omitted.

Normals are provided by the two-dimensional list Normals, where

the first dimension of the two-dimensional list addresses the corresponding list of vertex indices of the triangular faces;
the second dimension of the two-dimensional list provides exactly three real values to determine the direction of the normal at this vertex of the triangle.

The indices in the CoordIndex point into the list of Normals. The indices of CoordIndex are applied to both points, either directly directly, or via the PnIndex and normals. See Figure 8.8.3.47.C for handling of normals.

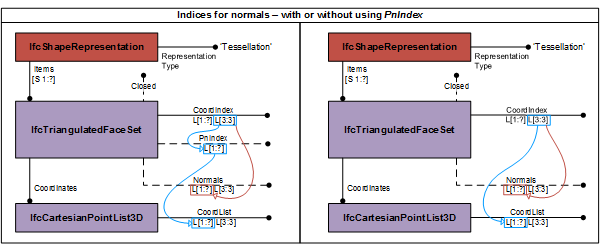
Figure 8.8.3.47.D shows the use of IfcTriangulatedFaceSet without annotation. The diagram of the IfcTriangulatedFaceSet represents the indices and the ordered list into which the indices point. The index starts with 1 (indexed as 1 to N), if the greatest index in CoordIndex in N, then the IfcCartesianPointList shall have N lists of 3:3 coordinates.

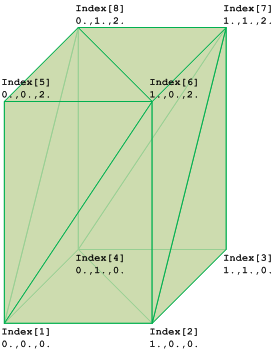
IfcTriangulatedFaceSet_Example-01 — Figure 8.8.3.47.D — Triangulated face set geometry

Figure 8.8.3.47.D shows an IfcTriangulatedFaceSet represented by:

CoordIndex:
((1,6,5), (1,2,6), (6,2,7), (7,2,3), (7,8,6), (6,8,5), (5,8,1), (1,8,4), (4,2,1), (2,4,3), (4,8,7), (7,3,4))

IfcCartesianPointList3D:
((0.,0.,0.), (1.,0.,0.), (1.,1.,0.), (0.,1.,0.), (0.,0.,2.), (1.,0.,2.), (1.,1.,2.), (0.,1.,2.))

Informal Propositions

If Closed = TRUE, the same topological constraints as imposed by an faceted boundary representation shall be safisfied. In particular:
each face shall be unique;
each edge shall be used by exactly two boundaries of faces;
the topological normal at each point on the boundary of the triangulated face set shall point away from the material of the solid.

8.8.3.47.2 Entity inheritance

8.8.3.47.3 Attributes

#	Attribute	Type	Description
IfcRepresentationItem (2)
	LayerAssignment	SET [0:1] OF IfcPresentationLayerAssignment FOR AssignedItems	Assignment of the representation item to a single or multiple layer(s). The LayerAssignments can override a LayerAssignments of the IfcRepresentation it is used within the list of Items. IFC2x3-CHANGE The inverse attribute LayerAssignments has been added. IFC4-CHANGE The inverse attribute LayerAssignment has been restricted to max 1. Upward compatibility for file based exchange is guaranteed.
	StyledByItem	SET [0:1] OF IfcStyledItem FOR Item	Reference to the IfcStyledItem that provides presentation information to the representation, e.g. a curve style, including colour and thickness to a geometric curve. IFC2x3-CHANGE The inverse attribute StyledByItem has been added.
IfcTessellatedFaceSet (4)
1	Coordinates	IfcCartesianPointList3D	An ordered list of Cartesian points used by the coordinate index defined at the subtypes of IfcTessellatedFaceSet.
	HasColours	SET [0:1] OF IfcIndexedColourMap FOR MappedTo	Reference to the indexed colour map providing the corresponding colour RGB values to the faces of the subtypes of IfcTessellatedFaceSet.
	HasTextures	SET [0:?] OF IfcIndexedTextureMap FOR MappedTo	Reference to the indexed texture map providing the corresponding texture coordinates to the vertices bounding the faces of the subtypes of IfcTessellatedFaceSet.
*	Dim	IfcDimensionCount	This attribute is formally derived. `3` The space dimensionality of this geometric representation item, it is always 3.
Click to show 6 hidden inherited attributes Click to hide 6 inherited attributes
IfcTriangulatedFaceSet (5)
2	Normals	OPTIONAL LIST [1:?] OF LIST [3:3] OF IfcParameterValue	An ordered list of three directions for normals. It is a two-dimensional list of directions provided by three parameter values. * The first dimension corresponds to the vertex indices of the Coordindex * The second dimension has exactly three values, [1] the x-direction, [2] the y-direction and [3] the z-directions
3	Closed	OPTIONAL IfcBoolean	Indication whether the face set is a closed shell (TRUE) or an open shell (FALSE). If omitted no such information can be asserted.
4	CoordIndex	LIST [1:?] OF LIST [3:3] OF IfcPositiveInteger	Two-dimensional list for the indexed-based triangles, where * The first dimension represents the triangles (from 1 to N) * The second dimension has exactly three values representing the indices to three vertex points (from 1 to 3). NOTE The coordinates of the vertices are provided by the indexed list of SELF\IfcTessellatedFaceSet.Coordinates.CoordList.
5	PnIndex	OPTIONAL LIST [1:?] OF IfcPositiveInteger	The list of integers defining the locations in the IfcCartesianPointList3D to obtain the point coordinates for the indices withint the CoordIndex. If the PnIndex is not provided the indices point directly into the IfcCartesianPointList3D.
*	NumberOfTriangles	IfcInteger	This attribute is formally derived. `SIZEOF(CoordIndex)` Derived number of triangles used for this triangulation.

Table 8.8.3.47.Q

8.8.3.47.4 Examples

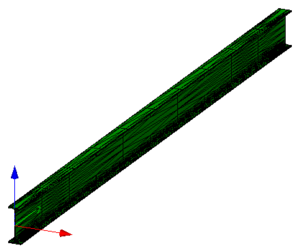
Figure 8.8.3.47.E

Beam Curved I Shape Tessellated
Figure 8.8.3.47.F

Tessellation With Blob Texture
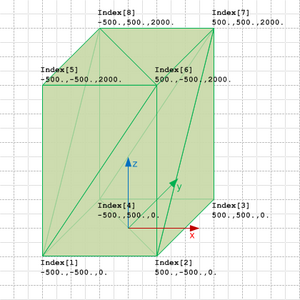
Figure 8.8.3.47.G

Slab Tessellated Unique Vertices
Figure 8.8.3.47.H

Triangulated Item
Figure 8.8.3.47.I

Tessellation With Image Texture
Figure 8.8.3.47.J

Geographic Referencing Utm
Figure 8.8.3.47.K

Geographic Referencing Gk
Figure 8.8.3.47.L

Beam Straight I Shape Tessellated
Figure 8.8.3.47.M

Tessellation With Pixel Texture
Figure 8.8.3.47.N

Basin Tessellation
Figure 8.8.3.47.O

Tessellation With Individual Colors
Figure 8.8.3.47.P

Column Straight Rectangle Tessellation

8.8.3.47.5 Formal representation

ENTITY IfcTriangulatedFaceSet
 SUPERTYPE OF (ONEOF
	(IfcTriangulatedIrregularNetwork))
 SUBTYPE OF (IfcTessellatedFaceSet);
	Normals : OPTIONAL LIST [1:?] OF LIST [3:3] OF IfcParameterValue;
	Closed : OPTIONAL IfcBoolean;
	CoordIndex : LIST [1:?] OF LIST [3:3] OF IfcPositiveInteger;
	PnIndex : OPTIONAL LIST [1:?] OF IfcPositiveInteger;
 DERIVE
	 NumberOfTriangles : IfcInteger := SIZEOF(CoordIndex);
END_ENTITY;